NJU-Static-Analysis-Data-Flow-Analysis-2
Live Variables Analysis
Live Variables 定义
活跃变量(Live Variables):
程序点p处的变量v是活变量,当且仅当在CFG中存在某条从p开始的路径,在这条路径上变量v被使用了,且在使用前未被重定义(但是不要求v在p之前必须被定义到)
可应用于寄存器分配(Register Allocation),可以作为编译器优化的参考信息。比如说,如果在某个程序点处,所有的寄存器都被占满了,而我们又需要用一个新的寄存器,那么我们就要从已经占满的这些寄存器中选择一个去覆盖它的旧值,我们应该更青睐于去覆盖那些储存死变量的寄存器。

使用bit vector来表示活跃变量中的数据流值
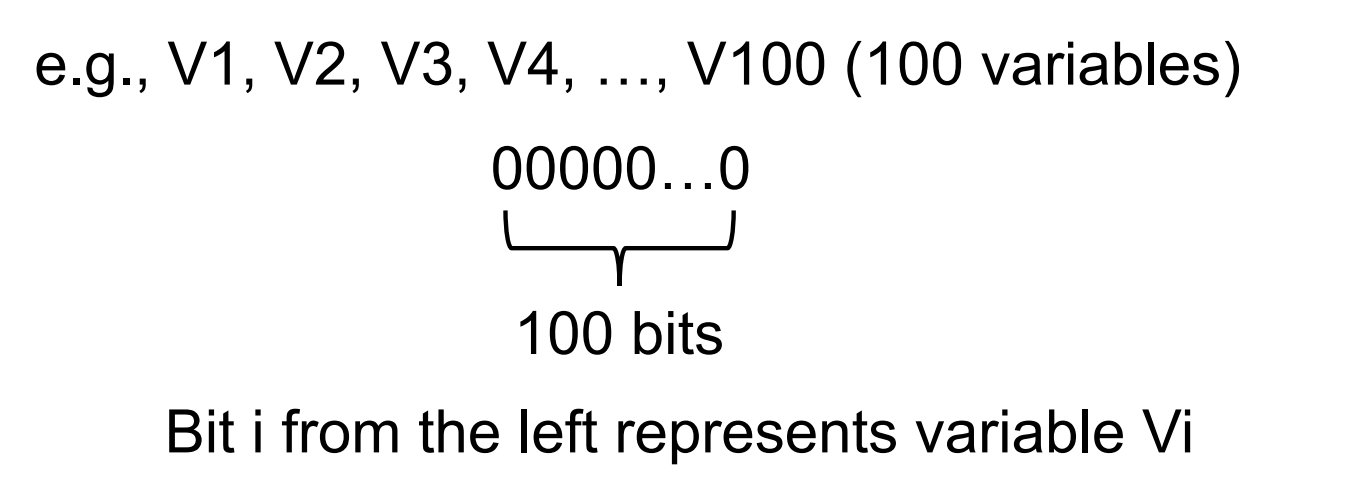
$V_i = 1$表示$i$对应的变量为活跃变量
Transfer function和control flow
- 一个例子:
主要是理解活跃变量的定义:
redefine之前进行use

4的那种情况可以拆解成先use再redefine
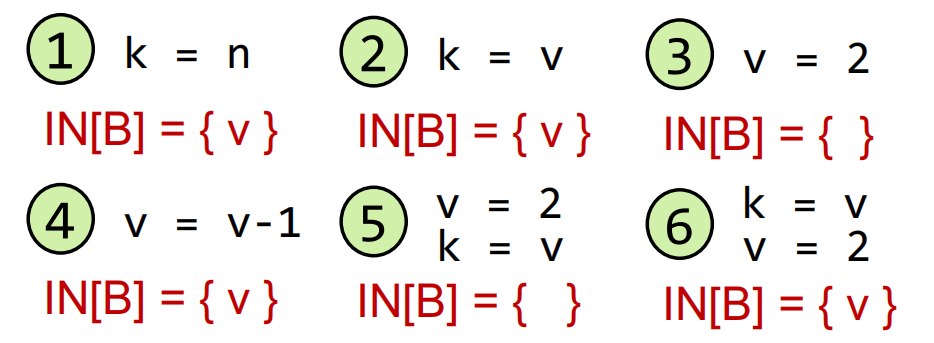
- 所以归纳出公式
$use_B$ 指在Basic Block $B$中在redefine之前use到的变量,在其对应的bit vector位置上记为1
$def_B$ 指在Basic Block $B$中在redefine对应的变量上,bit vector置为1,并为kill操作做准备

活跃变量分析算法
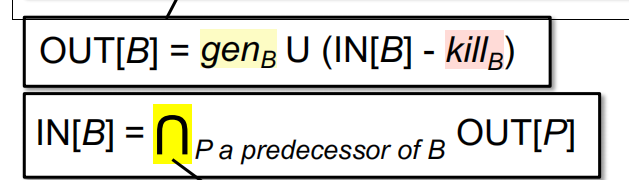
也是一个Iteration的算法,所以开头的初始化按照模板来走,分成了两部分
接下来就是对每个$OUT[B]$和$IN[S]$的声明了

例子详情见ppt,讲得很通俗易懂
Available Expression Analysis
Available Expression 定义
可用表达式分析(Available Expression):
表达式
x op y在程序点p是可用的 <=>
- 所有程序入口点到程序点p的路径都必须经过
x op y表达式的Evaluation- 在最后一次
x op y的评估之后,没有x或者y的重定义对于程序中每个程序点处的可用表达式分析,称之为 可用表达式分析(Available Expression Analysis)
available expression是一种优化层次上的数据流分析对象,由于是优化,不可错报可以漏报,是一种must analysis。
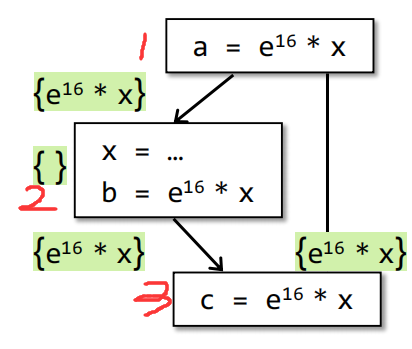
考虑如下这个例子:
在1处定义了一个表达式,其中的表达式为$e^{16}*x$,在$BB_2$后,即使先对$x$进行重定义,但是之后仍旧使用了$b = e^{16} * x$,因此$b = e^{16} * x$仍旧是available,最后让两条edge上的PP做交,可以得到汇入$BB_3$的表达式状态
Transfer function和control flow
可用表达式的分析算法
值得注意的点如下:
整个算法在控制流图中的分析方向:从entry自顶向下按顺序分析,入口点处的$OUT[entry]=null$
对于其他PP处的$OUT[B]$设置为全1
在控制流汇聚的时候,对于$OUT[B]$的处理需要做interaction,作为下一个$BB$的输入

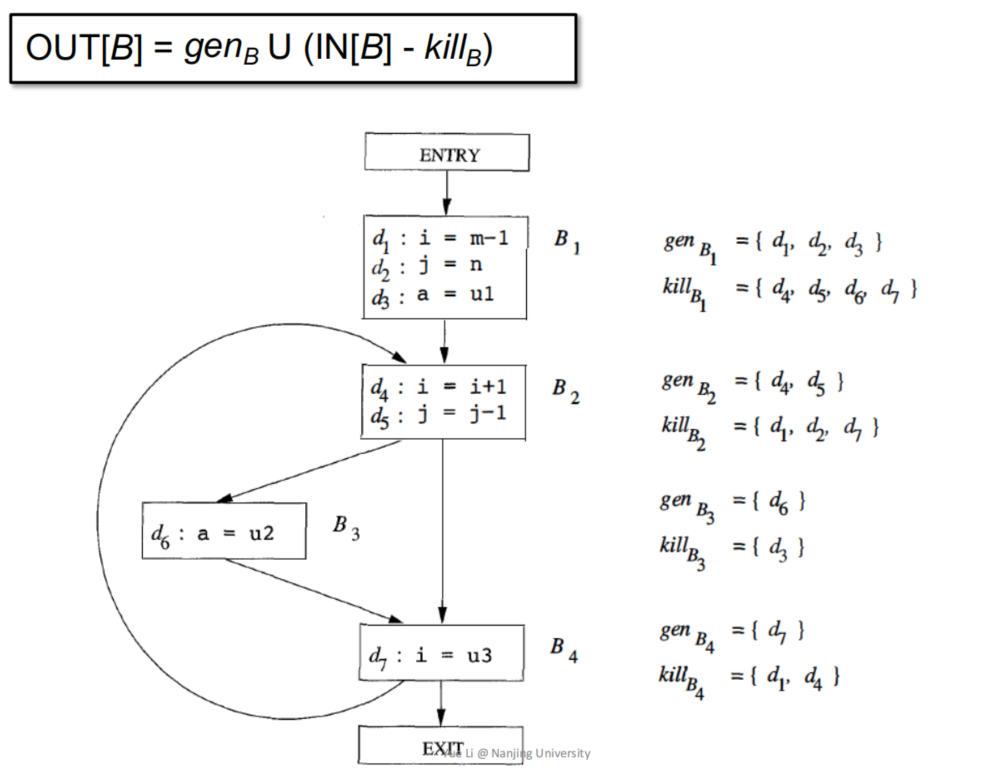
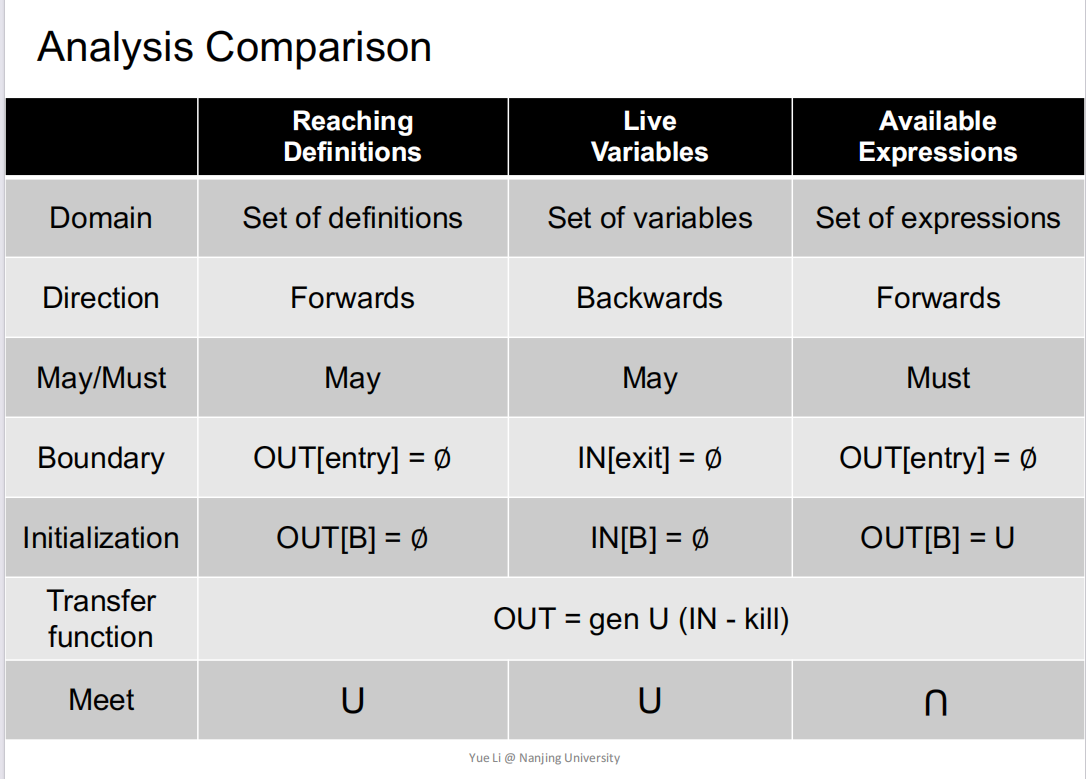
三种数据流分析的比较
这里重点回顾下 到达定值分析 和 活跃变量分析,感觉这两个分析对象很容易混淆
- 到达定值分析和活跃变量分析都是以并集作为交汇运算,我们主要关心的是其中一条路径上是否满足我们所想要的性质,而不关心所有路径
- 活跃变量分析是逆向遍历的(从exit为分析入口点,与控制流方向相反),且针对的是某个变量,关注的是程序点p上的对变量x的使用可以被传递到在某个执行路径中p之前的所有程序点。
- 到达定值分析,正向分析,针对的是definition,我们关注的是程序点p上的definition对于x的定义是否可以传播到某条执行路径中的且在p之后的程序点。